📑 문제
문제 설명
n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 노드의 개수 n은 2 이상 20,000 이하입니다.
- 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
- vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
입출력 예
n/ vertex/ return
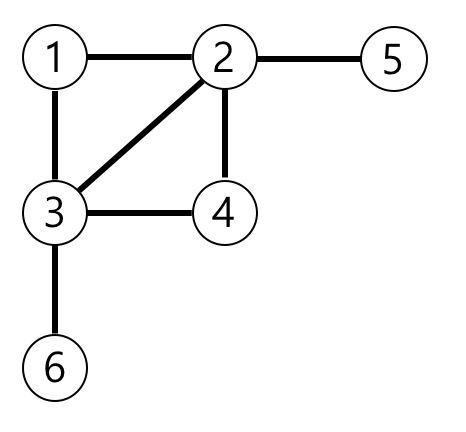
| 6 | [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] | 3 |
입출력 예 설명
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.
✒️ 풀이
❗ 노드 개수만큼 배열을 만들려다가 복사 실수를 해서 쓸데없는 애를 먹었던 문제였다.
[[0]]을 곱하기로 N개를 만들면, [[0], [0] ... ] 원하는 모양은 나오지만, 결과적으로 똑같은 주소값이 늘어난 것이기 때문에 입출력이 모든 내부 배열에 똑같이 일어나는 참사가 난다.
그렇기 때문에 이차원 배열을 만들 때에는 for문을 이용해서 추가해주는 코드를 사용해야 한다.
graph = [[0] for _ in range(n+1)]
💡1번부터 출발했을 때, 깊이가 가장 노드 개수를 찾는 문제이다.
하나의 큐에 인풋/아웃풋이 일어나기 때문에, 깊이를 다룰 때에는 모든 깊이를 돌며 각 깊이에 있는 노드 개수만큼 인접노드를 탐색하고 추가해주는 작업을 해야한다.
🙋♀️ 의견
개념을 처음부터 다시 잡고자 고른 전형적인 그래프 문제이다.
자바로는 많이 해봐서 일부러 파이썬으로 풀어봤다. ㅎㅎ 잘한 것 같다. 배열복사 실수도 있었으니....
💻 소스코드: 파이썬(Python)
from collections import deque
def solution(n, edge):
# [[0]]* (n+1)로 하면 주소값을 복사해서 2차원 배열을 만들기 때문에 값이 한번에 바뀌어버린다.
# * 쓰지말기
graph = [[0] for _ in range(n+1)]
visit = [0]*(n+1)
queue = deque()
for v1, v2 in edge:
graph[v1].append(v2)
graph[v2].append(v1)
queue.append(1)
visit[1] = 1
while queue:
answer = len(queue)
for _ in range(depth):
cur = queue.popleft()
for v in graph[cur][1:]:
if visit[v]==0:
queue.append(v)
visit[v]=1
return answer
# 예제
n = 6
vertex = [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]
# 출력
print(solution(n, vertex))
💎 💎 💎

Posted By SAY
𝘛𝘩𝘢𝘯𝘬𝘴 𝘧𝘰𝘳 𝘳𝘦𝘢𝘥𝘪𝘯𝘨
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스 스터디 7주차] 그래프 순위 Lv.3 - 파이썬(Python) / set 함수 활용 (0) | 2021.09.30 |
|---|---|
| [프로그래머스 스터디 7주차] 동적계획법 정수삼각형 Lv.3 - 파이썬(Python) (0) | 2021.09.30 |
| [프로그래머스 스터디 6주차] 이분탐색 입국심사 Lv.3 - 파이썬(Python) (0) | 2021.09.30 |
| [프로그래머스 스터디 6주차] 힙 이중우선순위큐 Lv.3 - 파이썬(Python) (0) | 2021.09.30 |
| [프로그래머스 스터디 6주차] 동적계획법 N으로 표현 Lv.3 - 파이썬(Python)/ DP (0) | 2021.09.30 |